V0

What is this?

The Elo system is based on the following philosophy - the relative rating of team A over team B must be indicative of the probability of victory team A has, over Team B. Elo may not be the best predictive tool for team sports, since it doesn't take into account player fatigue, injuries, players shifting teams between seasons, etc, unless they begin reflecting in match results. But nevertheless, Elo is an excellent rating system that increasingly more and more sports are adopting. For further understanding of Elo and how it works, do check out the Wikipedia page and Five Thirty Eight's articles 1 and 2.

Task 1 - Estimate value of K and Inter Season Carry Over % (C%)

The formula for Elo used for two teams A and B, is :

$$Elo\_New_A = {Elo\_Old_A + K * (Actual\_Outcome_A - Predicted\_Outcome_A)}$$ Where,

$$Predicted\_Outcome_A = {1 \over {1+10^{(Elo_B-Elo_A) \over 500}}}$$

All teams begin with 1000 points, and a factor of 500 has been chosen in the formula for scaling, since every 100 points difference translates to ~10% increase in probability of victory. The objective function considered to determine the value of K and C% is : $$Minimize : Sum([Difference\_in\_Prediction\_of\_Team\_A] * [Difference\_in\_Prediction\_of\_Team\_B])$$ Upon plotting the error function over a range of values of K and c%, we obtain the lowest cumulative error at K = 18 and C% = 100%

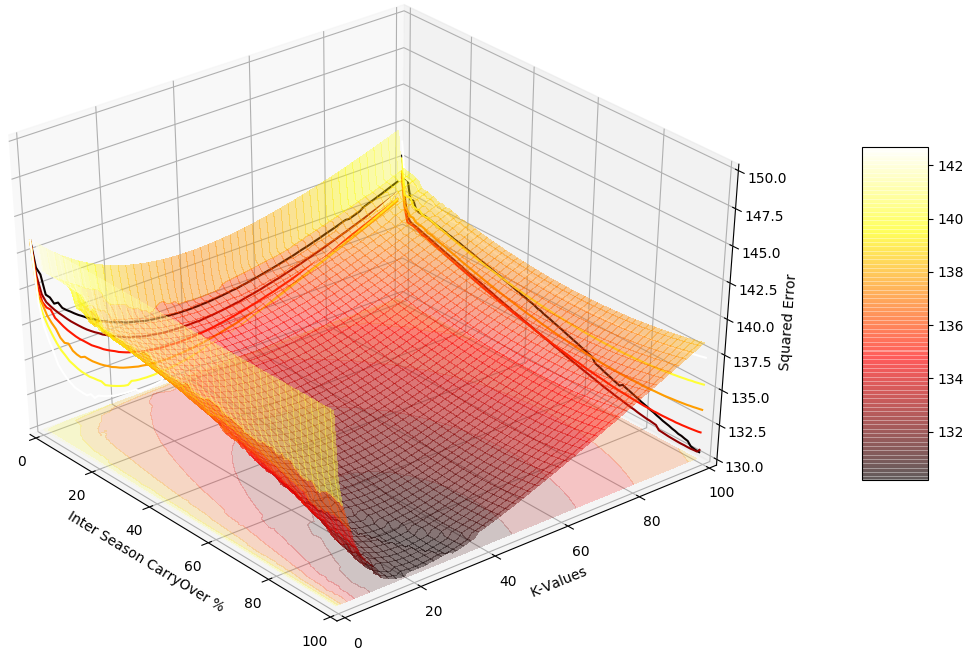
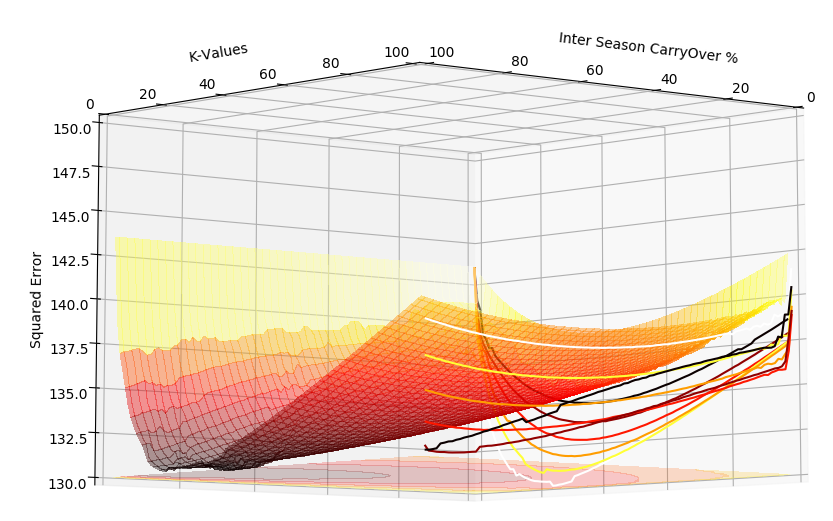
Now, with K = 18 and C% = 100%, the ELO ratings are as follows [Only till 2016 IPL]